4018. Turtle
There is a turtle in the left top corner of
rectangular table of size n × m. Each cell of the table contains some
amount of acid. Turtle can move right or down, its route terminates in right
bottom cell of the table.
Each milliliter of acid brings turtle some
amount of damage. Find the smallest possible value of damage that will receive
a turtle after a walk through the table.
Input. First line contains two positive integers n and m, no more than 1000 – the sizes of the table. Then n lines
are given, each contains m integers –
the description of the table, each number given the amount of acid in the cell
(in milliliters).
Output. Print the minimum possible damage for the
turtle.
|
Sample
input |
Sample
output |
|
3 4 5 9 4 3 3 1 6 9 8 6 8 12 |
35 |
SOLUTION
dynamic programming
Algorithm analysis
Let a[i][j] contains the amount
of damage for the turtle after visiting the cell (i, j). Let dp[i][j]
contains the minimum possible damage for the turtle during the route from (1, 1) to (i, j).
Consider the base cases:
·
dp[1][1] = a[1][1];
·
dp[i][1] = dp[i – 1][1] + a[i][1], 1 < i ≤ n (first column);
·
dp[1][j] = dp[1][j – 1] + a[1][j], 1 < j ≤ m (first row);
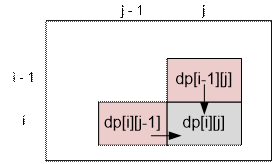
One can get into the cell (i, j)
either from (i – 1, j) or from (i, j –
1). Since the damage is minimized, then
dp[i][j] =
min(dp[i – 1][j], dp[i][j – 1]) + a[i][j]
Sample
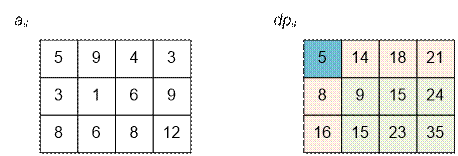
First column:
·
dp[2][1] = dp[1][1] + a[2][1] = 5 + 3 = 8,
·
dp[3][1] = dp[2][1] + a[3][1] = 8 + 8 = 16.
First row:
·
dp[1][2] = dp[1][1] + a[1][2] = 5 + 9 = 14,
·
dp[1][3] = dp[1][2] + a[1][3] = 14 + 4 = 18.
Calculate the
values of some non-border cells:
dp[2][2] = min(dp[1][2], dp[2][1]) + a[2][2] = min(14, 8) + 1 = 8 + 1 = 9
dp[3][4] = min(dp[2][4], dp[3][3]) + a[3][4] = min(24, 23) + 12 = 23 + 12 = 35
The desired path
for the turtle is:
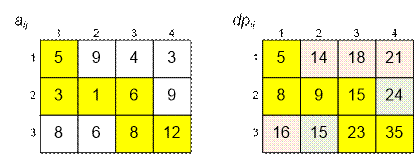
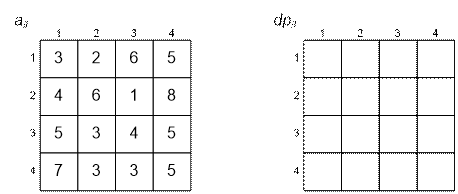
Exercise
Given matrix a[i][j], find the values of
matrix dp[i][j].
Algorithm realization
Declare the arrays.
#define MAX 1010
int a[MAX][MAX],
dp[MAX][MAX];
Read the input data.
scanf("%d %d",
&n, &m);
for (i = 1; i <= n; i++)
for (j = 1; j <= m; j++)
scanf("%d",
&a[i][j]);
Initialize the first row and the first column of array dp.
dp[1][1] = a[1][1];
for (i = 2; i <= n; i++)
dp[i][1] =
dp[i - 1][1] + a[i][1];
for (j = 2; j <= m; j++)
dp[1][j] =
dp[1][j - 1] + a[1][j];
Find the minimum possible damage for the
turtle for each cell.
for (i = 2; i <= n; i++)
for (j = 2; j <= m; j++)
dp[i][j] =
min(dp[i - 1][j], dp[i][j - 1]) + a[i][j];
Print the answer.
printf("%d\n",
dp[n][m]);
Java realization
import java.util.*;
class Main
{
static int a[][] = new int[1001][1001];
static int dp[][] = new int[1001][1001];
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = con.nextInt();
dp[1][1] = a[1][1];
for (int i = 2; i <= n; i++)
dp[i][1] = dp[i - 1][1] + a[i][1];
for (int j = 2; j <= m; j++)
dp[1][j] = dp[1][j-1] + a[1][j];
for (int i = 2; i <= n; i++)
for (int j = 2; j <= m; j++)
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + a[i][j];
System.out.println(dp[n][m]);
con.close();
}
}